Minutes
Meeting:
- Thorsten should type:
darcs get http://sneezy.cs.nott.ac.uk/darcs/termcd termchmod +x Setup.hs./Setup.hs configure --prefix=$HOME./Setup.hs build./Setup.hs install --user- (and providing $HOME/bin is in your path:)
epigram
- The next job in term is to build equality in these steps:
- Propositional equality
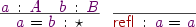
coersions between equal types (and the proof that these are coherant)

and the structural rule for application
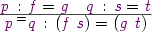
- Proof-irrelevance for equality, to do this right we need to decide equality during evaluation (if we do not have a proof of an equation but it’s homogeneous, then we win anyway). The upshot is Equality.lhs and
evalfrom Term.lhs need to be in the same file. - Observational equavalence, at some point (sooner rather than later) we’ll include the structural rule for
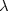 :
:

Thorsten pointed out that is rule can be derived from substution of equals for equals plus the more primitive:
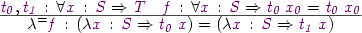
Having this gives OTT a simpler core, but Conor prefers the first version because it is easier to program with.
- Propositional equality